斐波纳奇序列

斐波纳奇序列
 

在《计算的书》中提出的一个数学问题产生了数字序列1，1，2，3，5，8，13，2l，34，55，89，144，如此无穷，这就是今天所知的斐波纳奇序列。这个问题是：

 

如果一对兔子从第二个月开始，每个月生一对新的兔子，而且不发生死亡，那么一对兔子在一年内总共会产生多少只兔子？

 

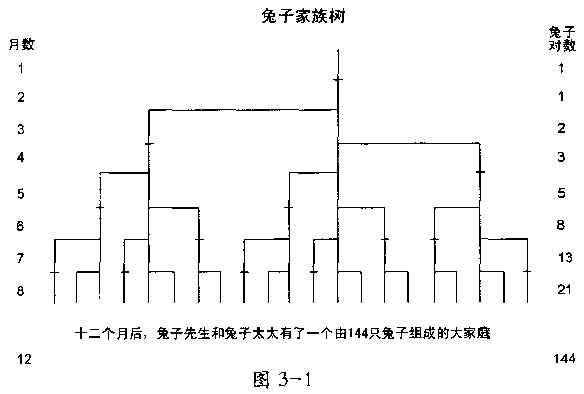
为了得到答案，我们发现每一对兔子，包括第一对，需要一个月的时间成熟，它们一旦可以生育，则每个月都会生出一对新兔子。在开始的头两个月的每一个月中，兔子的对数是一样的，所以序列是1，1。第一对兔子最终在第二个月使兔子的数量翻番，所以在第三个月开始时，就有了两对兔子。在这两对兔子中，老兔子在接下去的一个月里又生了一对新的兔子，这样就有了三对兔子，所以在第四个月的开头，序列扩大到了1，1，2，3。在这三对兔子中，两对老兔子，而不是那对最年轻的兔子，又可以生出新兔子，这样兔子就扩大到了五对。在下一个月里，有三对可以生育，所以序列扩大到了1，1，2，3，5，8，依此类推。图3—1是以对数加速度膨胀的兔子家族树。让序列这样发展几年，就会产生天文数字。比如，100个月后，我们就会得到354,224,848,179,261,915,075对兔子。由兔子问题产生的斐波纳奇序列有着许多有趣的特性，而且反映出序列中的各项几乎有着恒定的关系。

 

序列中任何两个相邻的数字之和形成了序列中的下一个更大的数字，即，1加1等于2，1加2等于3，2加3等于5，3加5等于8等等，至无穷。